前中后缀表达式

包子不会捏

虽然二狗也不会, 但二狗想在包子面前装b捏

本文只讨论所有运算符都是双目运算符的情况

概念

中缀表达式: 将操作符放在操作数中间的算术表达式, 与我们平时见到的一样

前缀表达式: 是指将运算符写在前面, 操作数写在后面的不包含括号的表达式, 又叫波兰表达式

后缀表达式: 是指运算符写在操作数后面的不包含括号的算术表达式，也叫做逆波兰表达式

表达式树

叶子节点为操作数, 其他节点为操作符, 无括号, 根据前中后序遍历可以得到对应的前中后缀表达式

eg:

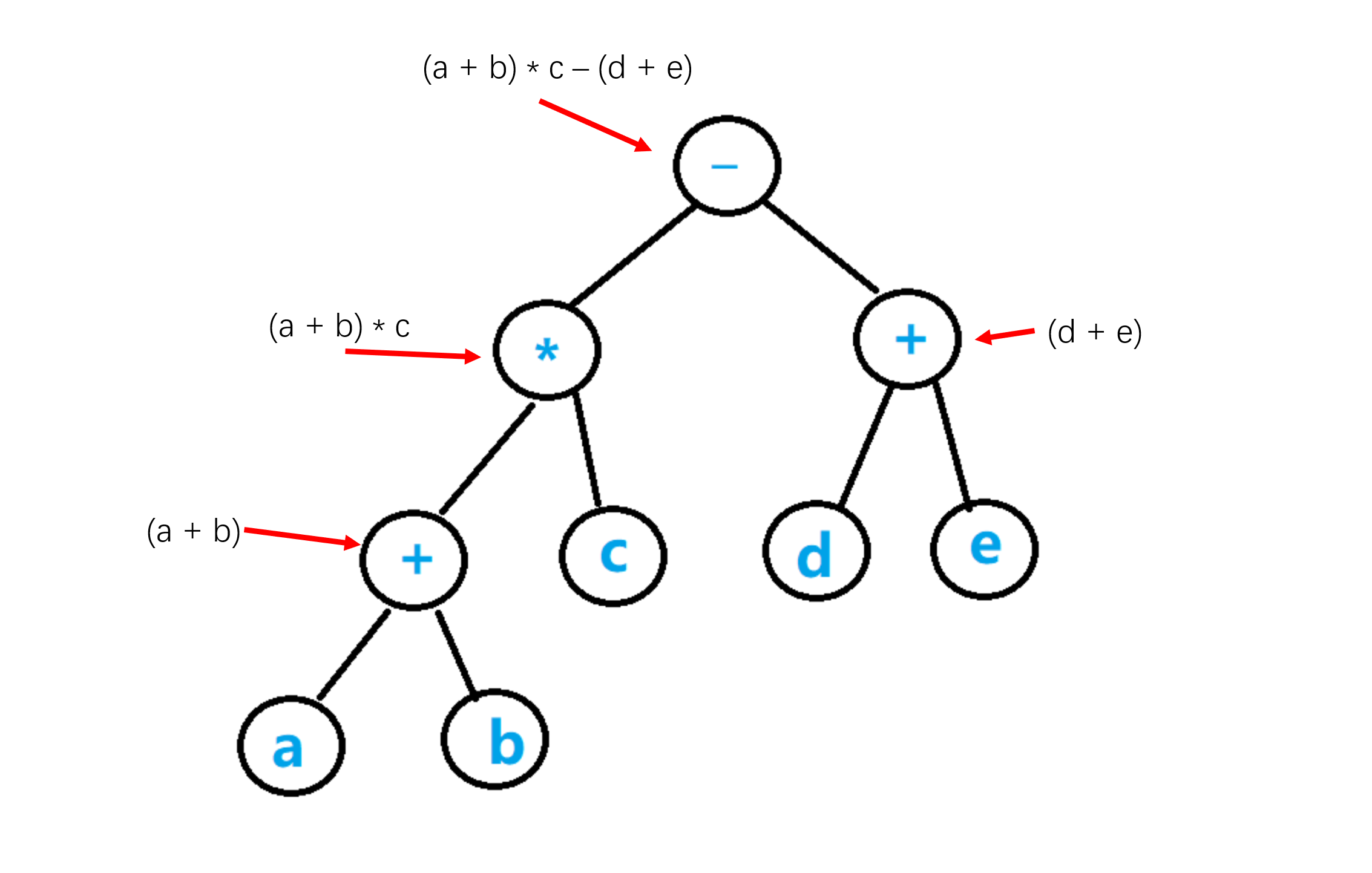
对于表达式 $(a+b)*c-(d+e)$

其对应的二叉树为

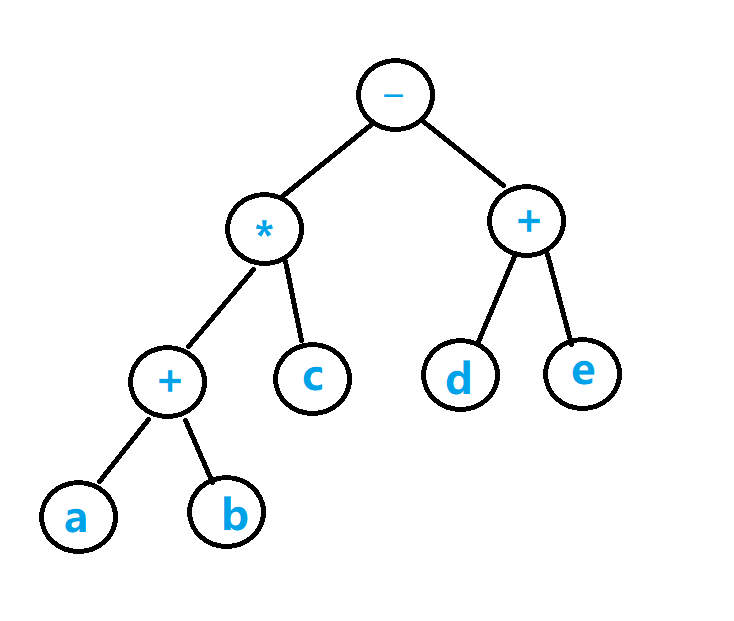
image-20221112203258793

前序遍历二叉树, 得到其前缀表达式$-*+abc+de$

中序遍历二叉树, 得到其本身$(a+b)*c-(d+e)$

后序遍历二叉树, 得到其后缀表达式 $ab+c*de+-$

表达式转二叉树

前缀表达式转二叉树

用一个栈存放表达式

遍历表达式, 若为操作符, 入栈

若为数字且栈顶也为数字, 弹出数字和操作符, 计算后入栈, 否则直接入栈

eg: 对于前缀表达式 $-*+abc+de$

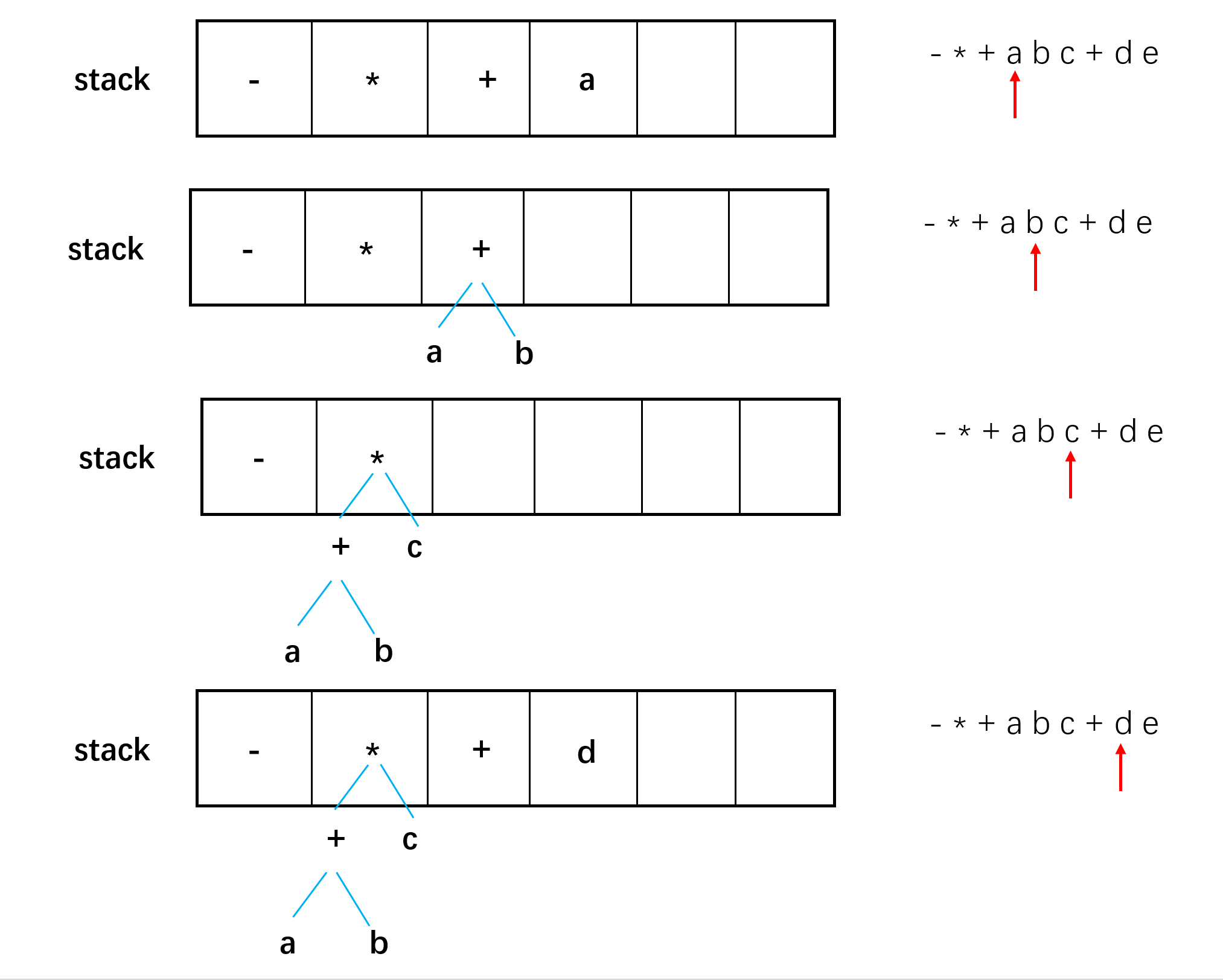
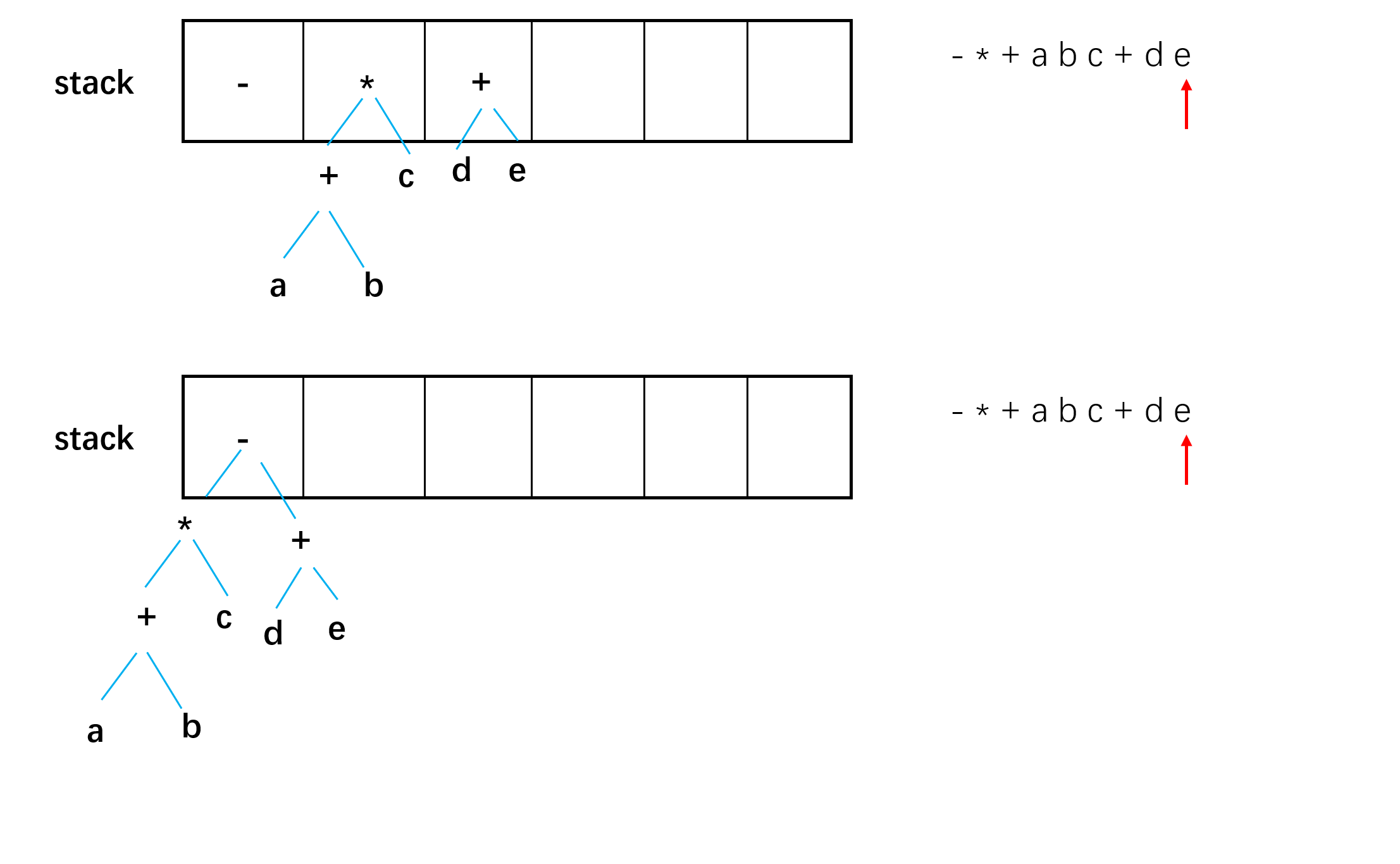
image-20221112222640555 image-20221112222934304

伪代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
stack<TreeNode*> st;
for(auto i: s){
    if(!isanum(i))
        st.push(new TreeNode(i));
    else{
        if(!st.empty() && isanum(st.top())){
            TreeNode* rs = new TreeNode(i);
            TreeNode* ls = st.top();
            st.pop();
            TreeNode* root = st.top();
            st.pop();
            
            root->left = ls;
            root->right = rs;
            st.push(root);
        }
    }
}

中缀表达式转二叉树

感觉应该可以正则后做, 但是二狗不会啦

二狗只会中缀转后缀 (后缀处理比前缀简单)

中缀转后缀是一个很经典的问题

从右到左进行遍历

运算数直接输出

遇到符号

为’(‘ 则直接输出, 为’)’则弹出直到为’(‘

为其他则与栈顶符号比较

若优先级高于栈顶, 则直接入栈

否则弹出, 直到栈为空或者栈顶优先级不高于此符号

1597. 根据中缀表达式构造二叉表达式树

由于给的结构体是char, 不考虑数的读取

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
/**
 * Definition for a binary tree node.
 * struct Node {
 *     char val;
 *     Node *left;
 *     Node *right;
 *     Node() : val(' '), left(nullptr), right(nullptr) {}
 *     Node(char x) : val(x), left(nullptr), right(nullptr) {}
 *     Node(char x, Node *left, Node *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    unordered_map<char , int > mp;
    stack<char> ss;
    stack<Node*> ans;
    vector<char> a;
    void pre()
    {
        mp['('] = 0; mp['+'] = 1; mp['-'] = 1;
        mp['*'] = 2; mp['/'] = 2; mp[')'] = 3;
    }
    void so()
    {
        for(auto i: a){
            if(i >= '0' && i <= '9') ans.push(new Node(i));
            else{
                Node* root = new Node(i);
                Node* rs = ans.top();
                ans.pop();
                Node* ls = ans.top();
                ans.pop();
                root->left = ls;
                root->right = rs;
                ans.push(root);
            }
        }
        
    }
public:
    Node* expTree(string s) {
        pre();
        
        for(auto i : s){
            if(i >= '0' && i <= '9')
            {
                a.push_back(i);
                continue;
            }
           
            
            if(i == ')'){
                while(ss.top() != '('){
                    char c = ss.top();
                    ss.pop();
                    a.push_back(c);
                }
                ss.pop();
            }
            else if(ss.empty() || mp[ss.top()] < mp[i] || i == '(') ss.push(i);
            else{
                while(!ss.empty()){
                    if(mp[i] > mp[ss.top()]) break;
                    char c = ss.top();
                    ss.pop();
                    a.push_back(c);
                }
                ss.push(i);
            }
        }

        while(!ss.empty()){
        a.push_back(ss.top());
        ss.pop();
        }
        so();
        return ans.top();
    }
};

后缀表达式转二叉树

用一个栈存放数字

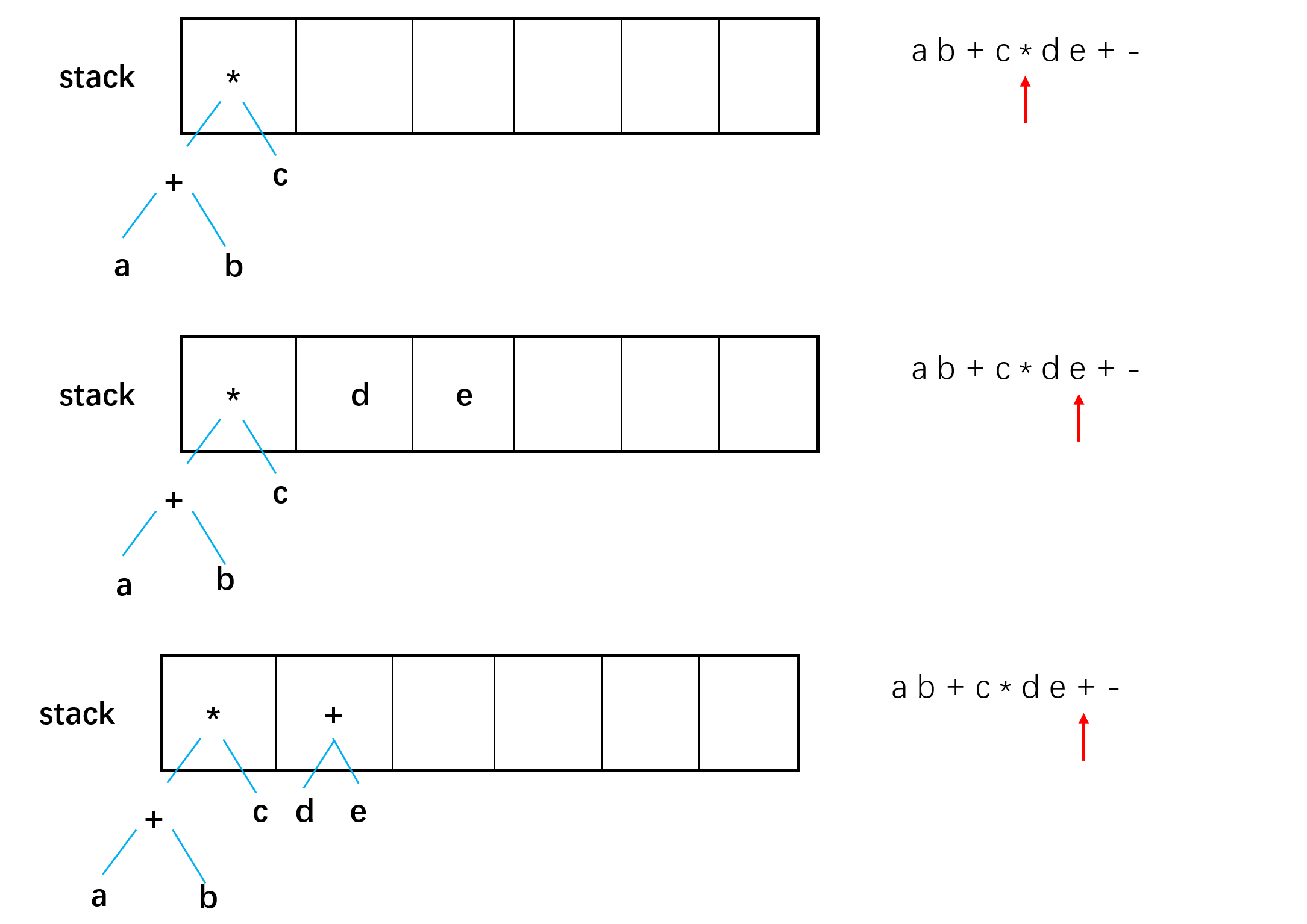
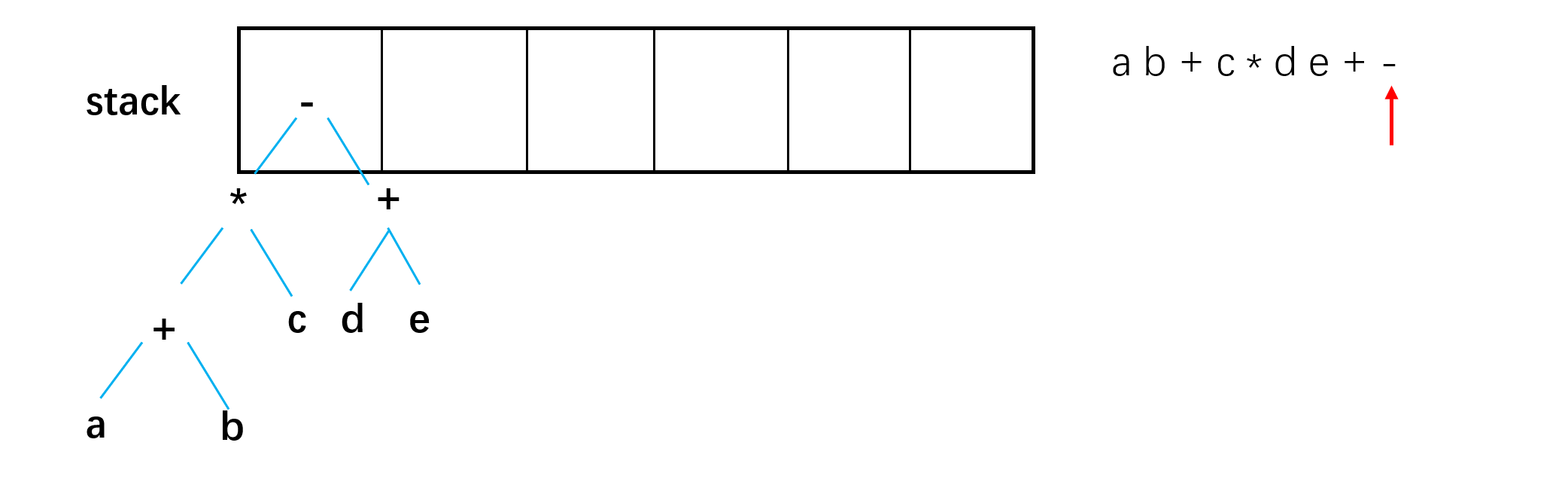
依次读入, 当读到数字时入栈, 读到符号时从栈顶取出两个数, 计算后入栈

eg: 对于后缀表达式 $ab+c*de+-$

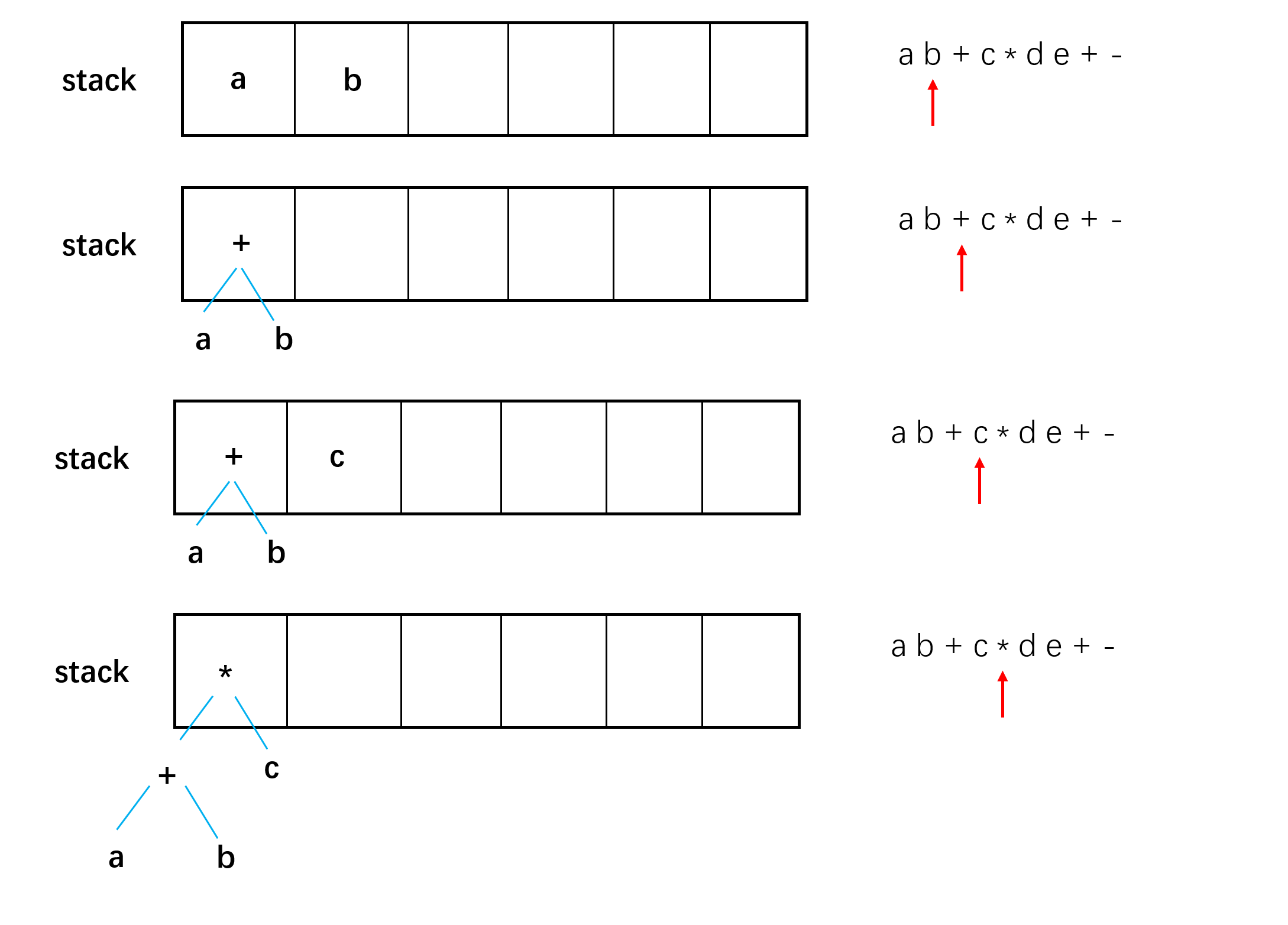
image-20221112215617340 image-20221112215954459 image-20221112220311446

伪代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
stack<TreeNode*> st;
for(auto i: s){
    if(isanum(i))
        st.push(new TreeNode(i));
    else{
        TreeNode* root = new  TreeNode(i);
        TreeNode* rs = st.top();
        st.pop();
        TreeNode* ls = st.top();
        st.pop();
        
        root->ls =ls;
        root->rs =rs;
        st.push(root);
    }
}
return st.top();

二叉树转表达式

对于前/后缀表达式, 由于没有括号, 所以只需要对树进行前/后序遍历即可

二叉树转中序表达式

不考虑化简情况

中序遍历二叉树, 对于每个非跟叶子节点, 给当前式子加一组括号即可

如何判断是否为根节点

可以在遍历前用一个全局变量记录根节点, 每次作比较

或者记录深度, 非0即可

伪代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
TreeNode* _root;
void so(TreeNode* root)
{
    if(!root) return ;
    if(root->left){
        if(root!= _root && root->right)
        cout<<"(";
        
        so(root->left);
	}
    
    cout<<root->val;
    
    if(root->right){
        so(root->right);
        
        if(root!=_root && root->left)
           cout<<")";
    }
}

//
void so(TreeNode* root, int dp)
{
    if(!root) return ;
    if(root->left){
        if(dp && root->right)
        cout<<"(";
        
        so(root->left, dp+1);
	}
    
    cout<<root->val;
    
    if(root->right){
        so(root->right, dp+1);
        
        if(dp && root->left)
           cout<<")";
    }
}

计算表达式的值

其实从叶子节点开始向上走, 每个非叶子节点的地方都是一个值, 根节点算出来就是最后的值

image-20221114211006295

所以, 表达式值的计算和表达式转换二叉数是一样的, 把建立父节点的过程变为计算值就行啦!