关于树
某次面试
-数据结构怎么样
-emmm,还行吧
-讲讲红黑树吧
-寄
只会对着板子抄线段树QAQ
总结一下二叉树相关吧
二叉排序树 (二叉搜索树/BST)
左子树的所有节点 < 根节点 < 右子树的所有节点 ( ls_max < r < rs_min )
它的左右子树也分别为二叉搜索树
没有相同的值
二叉搜索树的插入
空树,就首先生成根节点;
不是空树就按照查找的算法,找到父节点,然后作为叶子节点插入,如果值已经存在就插入失败
二叉搜索树的删除
如果删除的是叶节点,可以直接删除
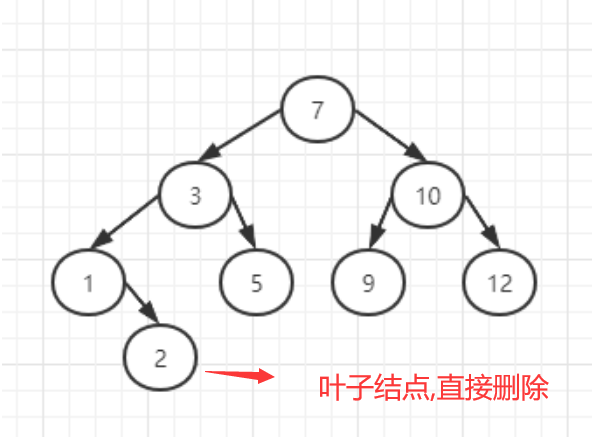
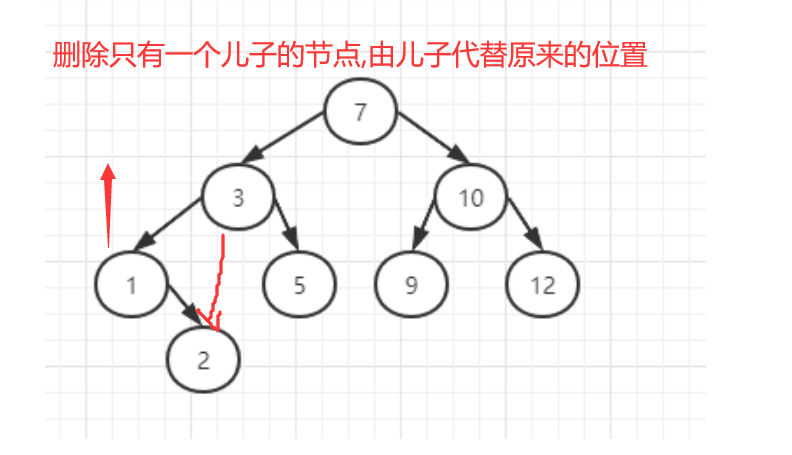
如果被删除的元素有一个子节点,可以将子节点直接移到被删除元素的位置
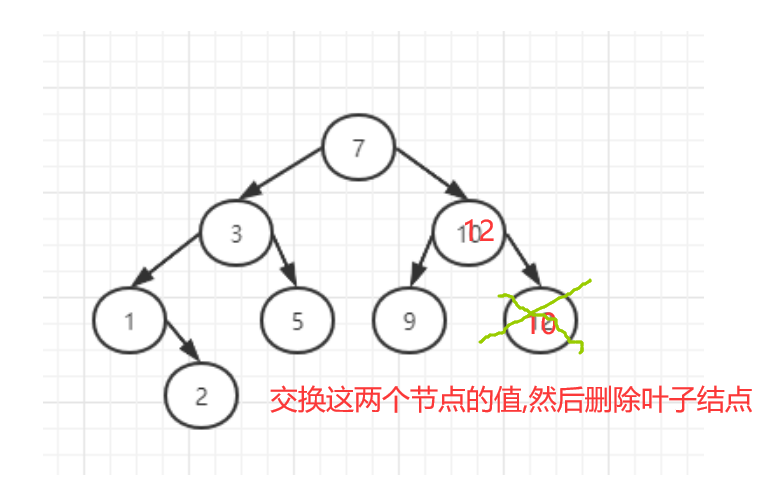
如果有两个子节点,这时候就采用中序遍历,找到待删除的节点的后继节点(或前驱节点),将其与待删除的节点互换,此时待删除节点的位置已经是叶子节点,可以直接删除
 |
|
插入删除复杂度
平均复杂度 $log_2N$
最坏情况: n ( 单链)
二叉搜索树的中序遍历为从小到大排序结果
哈希表与二叉查找树
哈希表中的数据是无序存储的,如果要输出有序数据序列,需要先进行排序,或者配合有序链表来使用。而对于二叉查找树,我们只需要进行中序遍历,就可以在O(n)的时间复杂度内,输出有序数据序列。
哈希表扩容耗时很多,而且当遇到哈希冲突时,性能不稳定。而对于二叉查找树,如果用平衡二叉树就非常稳定,时间复杂度稳定在O(logn)
O(logn)的算法并不一定比O(1)的算法运行速度慢。尽管哈希表上操作的时间复杂度是常量级的,但因为哈希冲突的存在,再加上哈希函数的计算耗时,哈希表并不一定就比平衡二叉树效率高。
哈希表的构造比二叉查找树复杂,需要考虑的东西很多,如哈希函数的设计、冲突解决方法、扩容和缩容等。平衡二叉树只需要考虑如何维护平衡性
平衡二叉树 (AVL树)
在二叉排序树的基础上,有
左子树和右子树的高度之差的绝对值小于等于1
左子树和右子树也是平衡二叉树
为了方便起见,给树上的每个结点附加一个数字,给出该结点左子树与右子树的高度差,这个数字称为结点的平衡因子(BF)
平衡因子=结点左子树的高度-结点右子树的高度
平衡因子 = {-1,0,1}
为什么会有平衡二叉树
因为二叉排序树在某些情况下的效率会达到 $o(n)$ ,这明显不是我们想要的结果 (链表不爽啊吗)
有了|BF| <= 1这个限制条件以后,就可以将复杂度控制在 $log_2N$ 左右了
左旋和右旋

左旋
右儿子变父亲
右儿子的左子树变父亲的右子树
右旋
左儿子变父亲
左儿子的右子树变左子树
平衡二叉树插入和调整
四种失衡类型
失衡是相对于平衡而言的,在插入新的节点后,会导致新树在原来的基础上失衡,这时就需要调整了
找最小的失衡子树的根节点作为失衡结点
最小失衡子树:距离插入节点最近的,且平衡因子的绝对值大于1的节点为根的子树
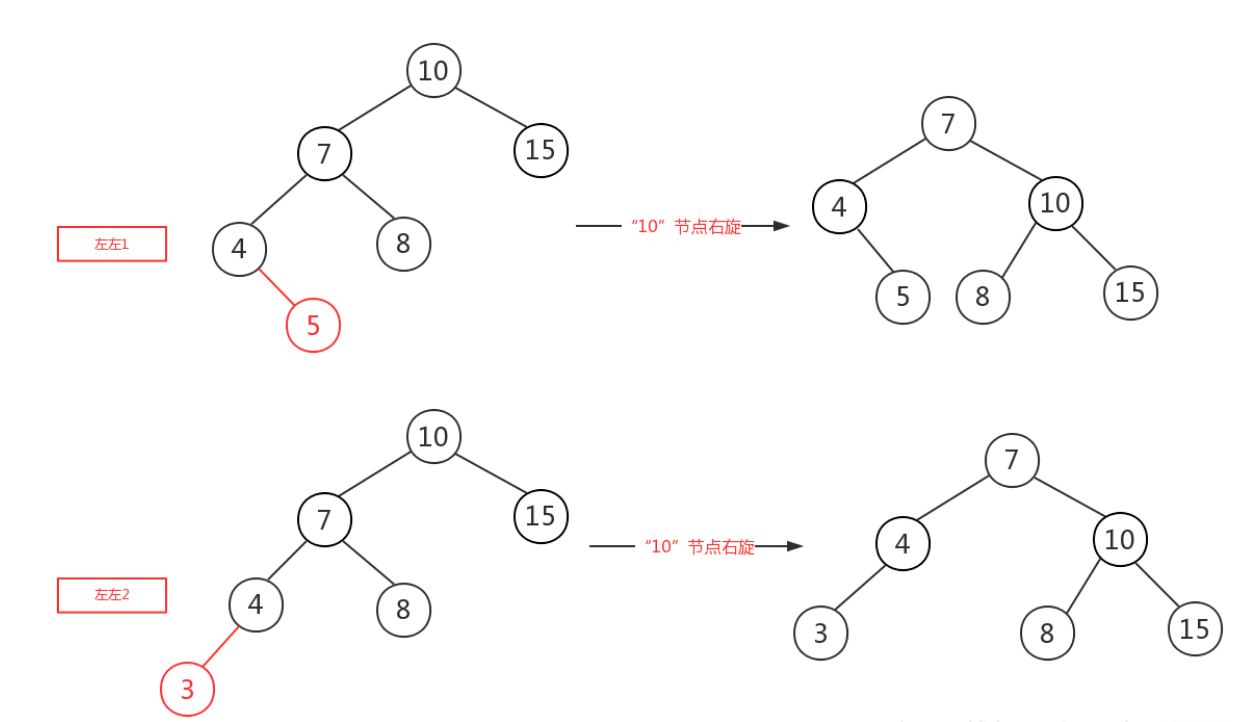
LL
在原来平衡的二叉树上,在节点的左子树的左子树下插入节点导致失衡
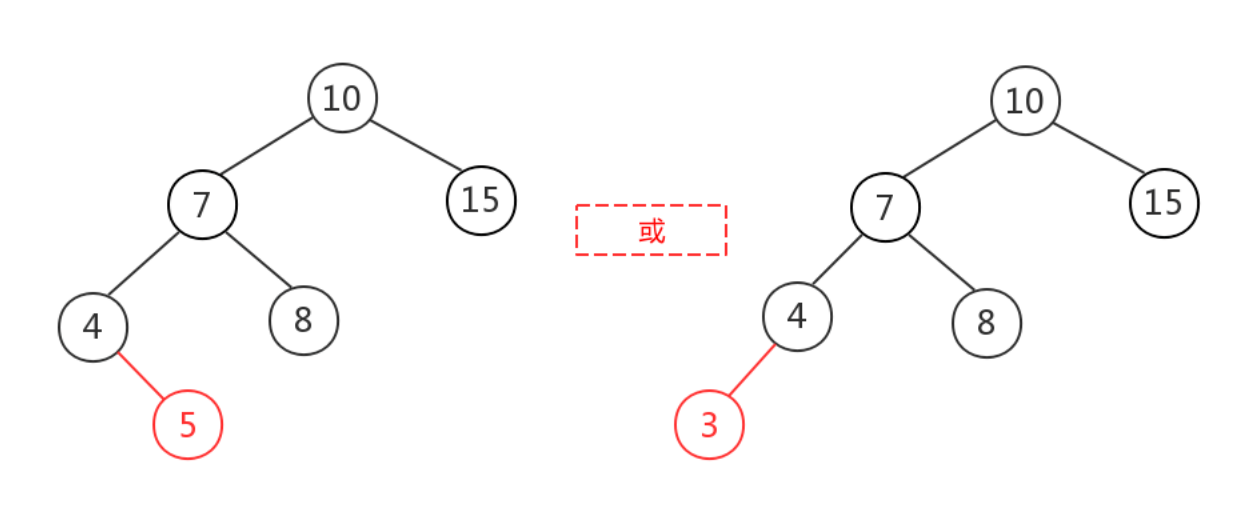
对节点进行右旋
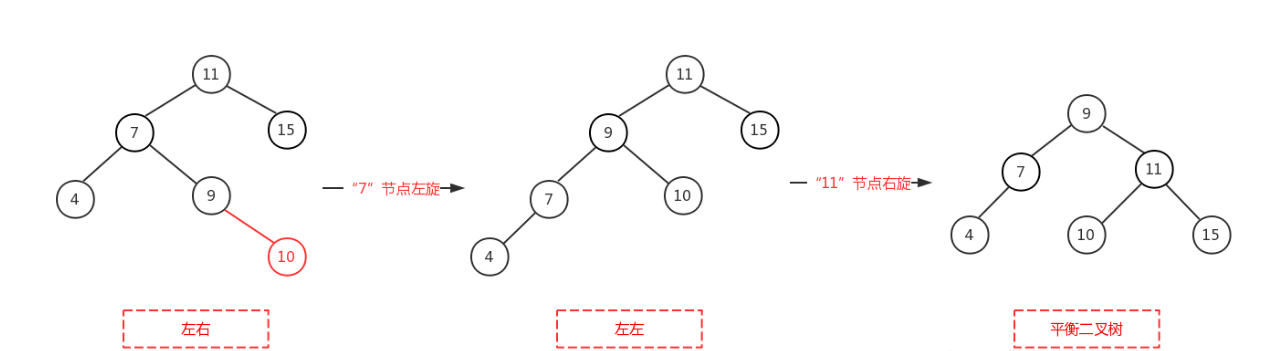
LR
原来平衡的二叉树上,在节点的左子树的右子树下插入节点导致失衡
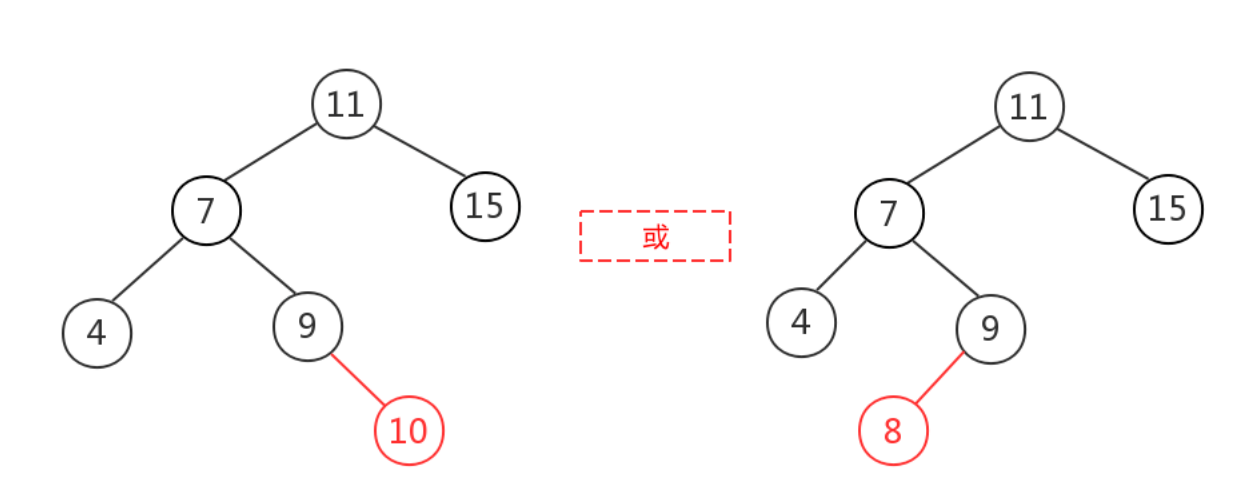
先对左儿子进行左旋,这时树就变为LL,然后对节点进行右旋
RR
在原来平衡的二叉树上,在节点的右子树的右子树下插入节点导致的失衡
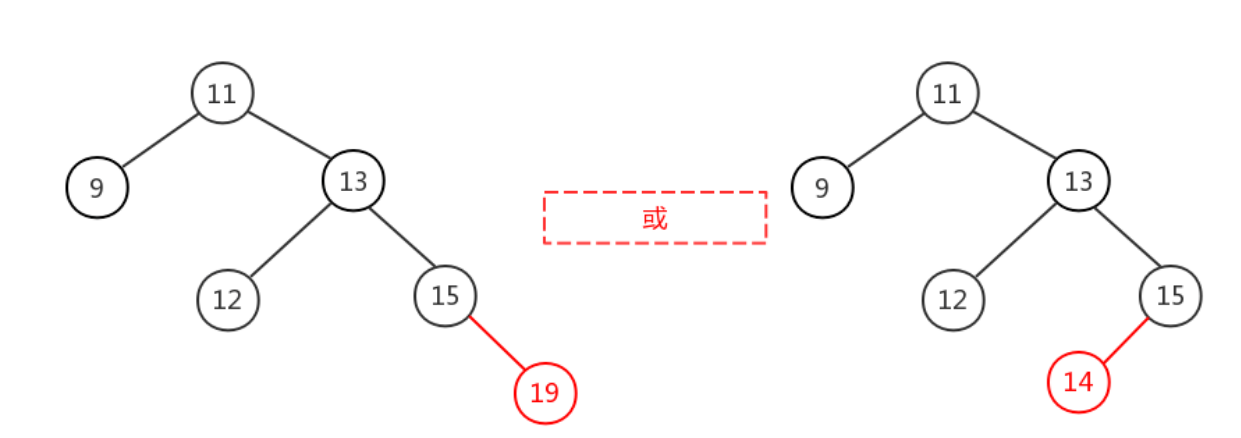
对节点进行左旋
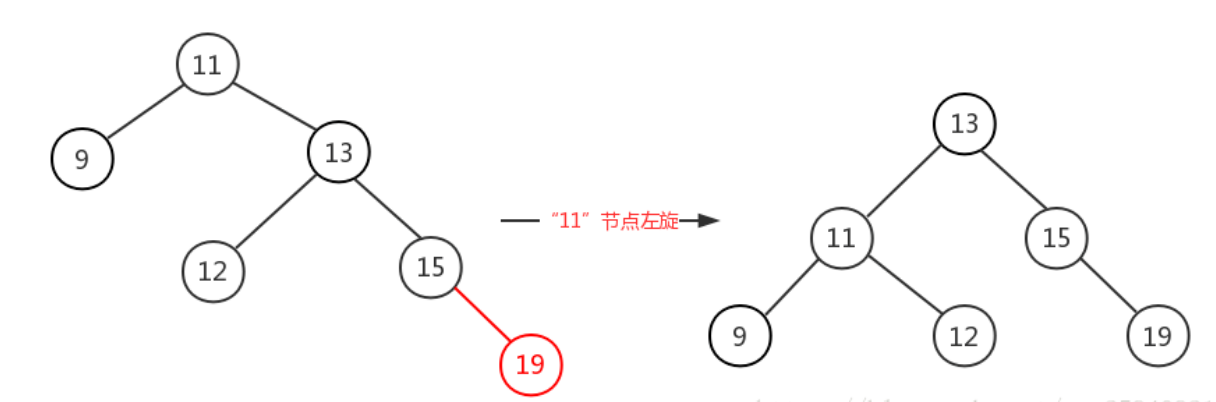
RL
在原来平衡的二叉树上,在节点的右子树的左子树下插入节点导致的失衡
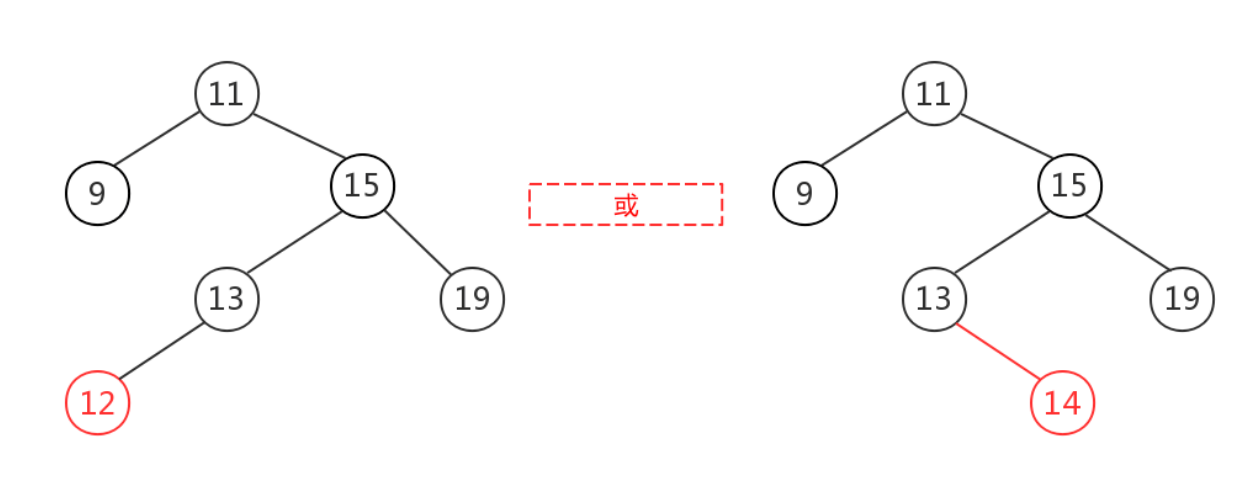
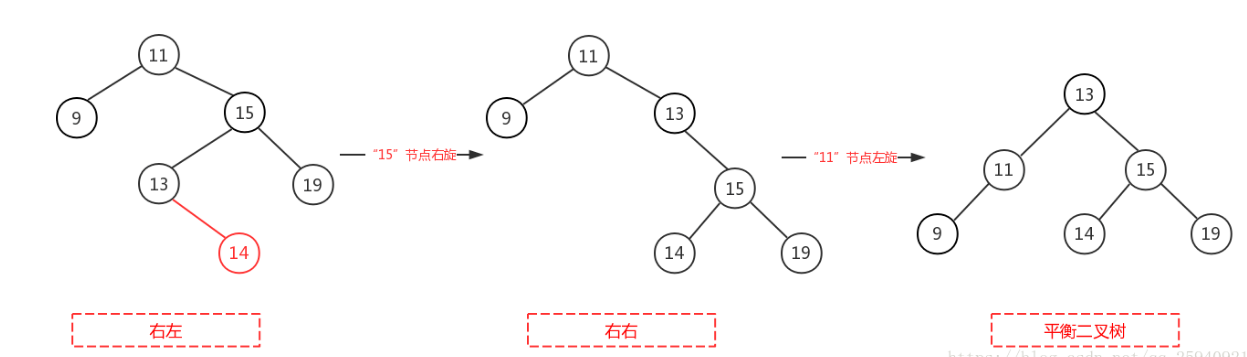
先对右节点进行右旋,这时变为RR,再对节点左旋
平衡二叉树删除节点
删除的步骤跟二叉排序树的删除差不多,删完后不断向上检查是否失衡,失衡就调整,直到根节点
红黑树
红黑树是一种特化的AVL树
与AVL树相比,红黑树牺牲了部分平衡性,以换取插入/删除操作时较少的旋转操作,整体来说性能要优于AVL树
红黑树通过变色和旋转来维护
红黑树特征
5大特征:
每个节点不是黑色就是红色
根节点为黑色
红色节点的父节点和子节点不能为红色 (不能有相邻的红色节点)
所有的叶子节点 (最底层不存放数据的节点) 都是黑色, 且为空
每个节点到叶子节点的每个路径黑色节点的个数都相等
为什么会有红黑树
AVL的左右子树高度差不能超过1,每次进行插入/删除操作时,几乎都需要通过旋转操作保持平衡
在频繁进行插入/删除的场景中,频繁的旋转操作使得AVL的性能大打折扣
红黑树通过牺牲严格的平衡,换取插入/删除时少量的旋转操作,整体性能优于AVL
红黑树插入时的不平衡,不超过两次旋转就可以解决;删除时的不平衡,不超过三次旋转就能解决
红黑树的红黑规则,保证最坏的情况下,也能在 $o(log_2N)$ 时间内完成查找操作
红黑树和AVL树
AVL树的查找效率更高, 但平衡调整的成本也更高
在需要频繁查找时, 选用AVL树
在需要频繁插入删除时,选择红黑树
红黑树的维护
插入
插入节点默认为红色
插入节点为根节点
将节点变为黑色
插入节点的父节点为黑色
此时红黑树性质没有被打破,不用管
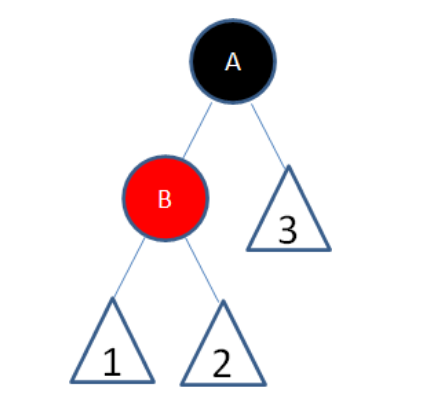
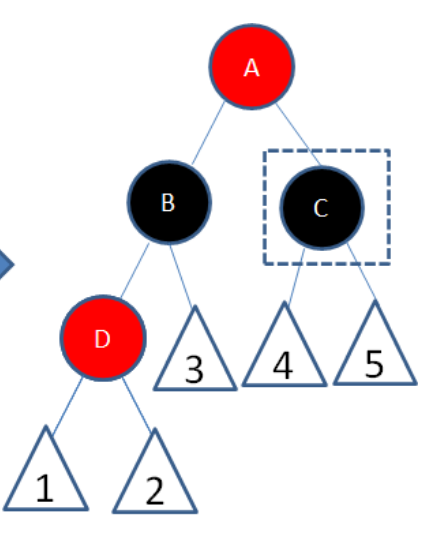
插入节点的父节点和叔节点都是红色
由于父节点和叔节点都是红色,所以爷爷一定是黑色
BD两个红色节点连在一起了,所以将A的黑色”下放”一层
即A变红,B,C变黑,这样就保证BC的路径上黑色节点数不变了
 |
|
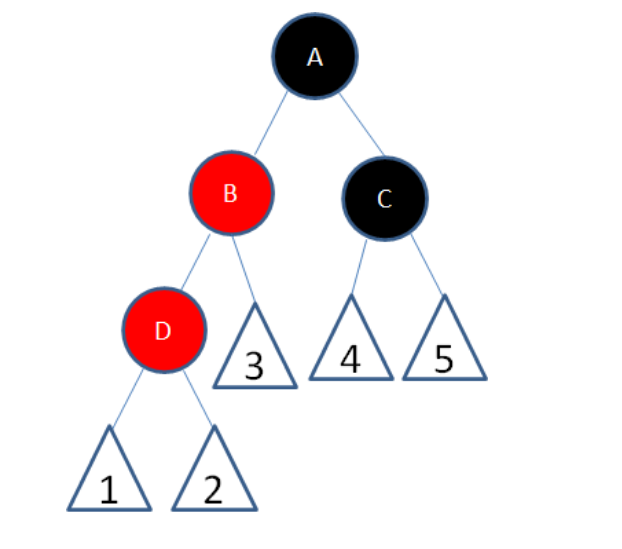
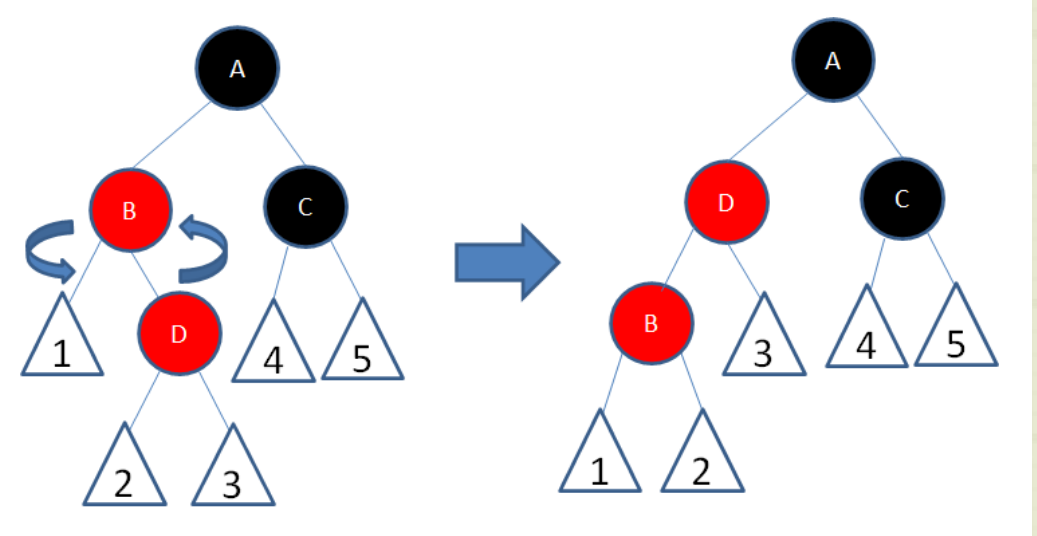
插入节点的父节点为红色,叔节点为黑色或没有叔叔
父节点为红色,爷爷一定为黑色
插入节点为左孩子
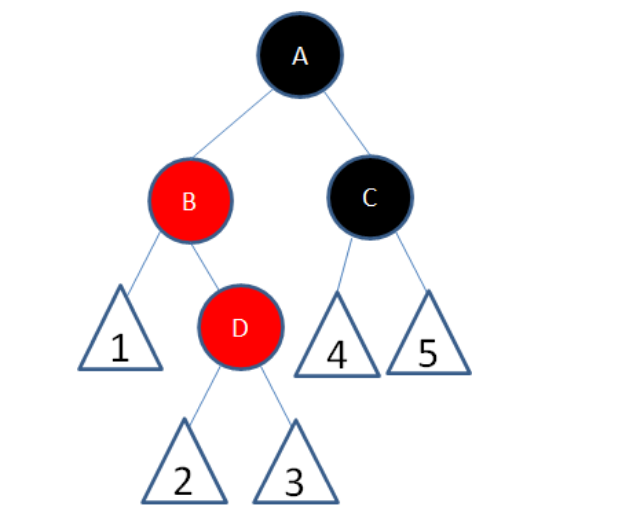
以爷爷为轴右旋,这时D路径少一个黑色,所以将A的黑色上一层
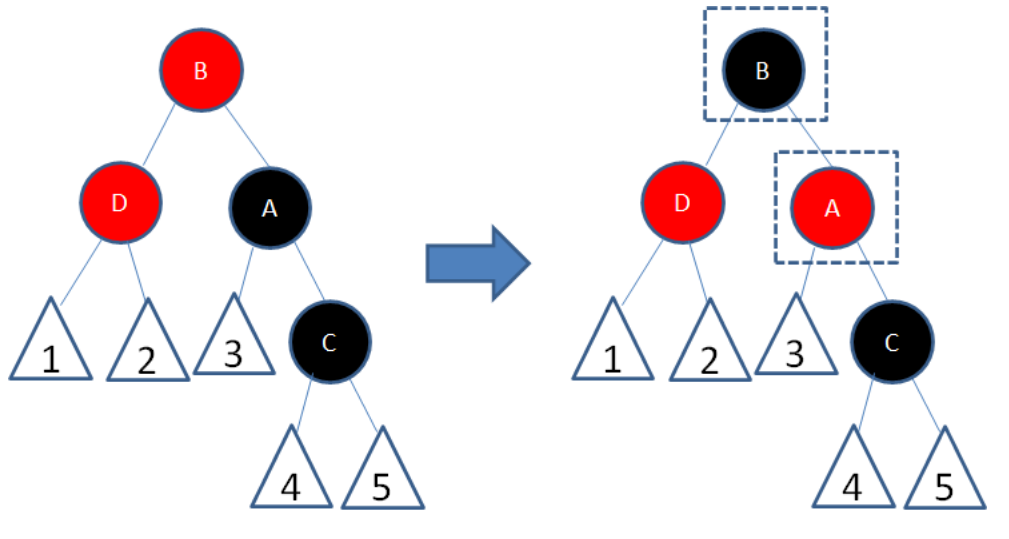
插入节点为右孩子
对插入节点左旋,变为上面的情况
删除
写在前面~~~~的废话
红黑树的删除比较复杂, 网上的教程讲的也不大致相同, 先按照我觉得自己可以理解的版本来写, 等我觉得我能完全讲清楚了再把这个重构一下
有两个儿子的节点, 将其后继节点的内容赋值给当前节点, 并删除其后继节点
对于没有儿子的节点, 只需要删除当前节点
对于有一个儿子的节点, 直接删除该节点, 并用其儿子节点代替该节点
对于有两个儿子的节点, 将其后继节点的内容赋值给当前节点, 并删除其后继节点
由树的性质可知后继节点没有儿子或者只有一个右儿子
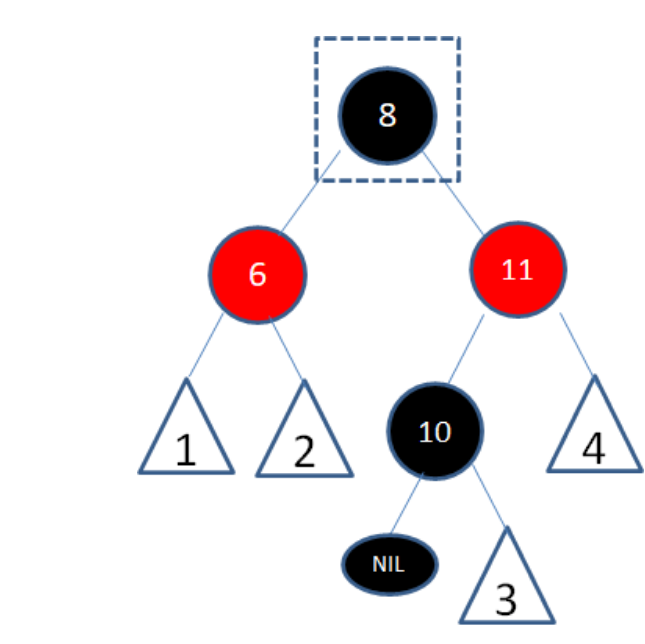
考虑下面的例子, 需要删除8节点, 找到它的后继节点10, 并将10的值赋给8, 此时由于只改变了值而没有改变颜色, 所以树的性质不变
接下来考虑删除10号节点
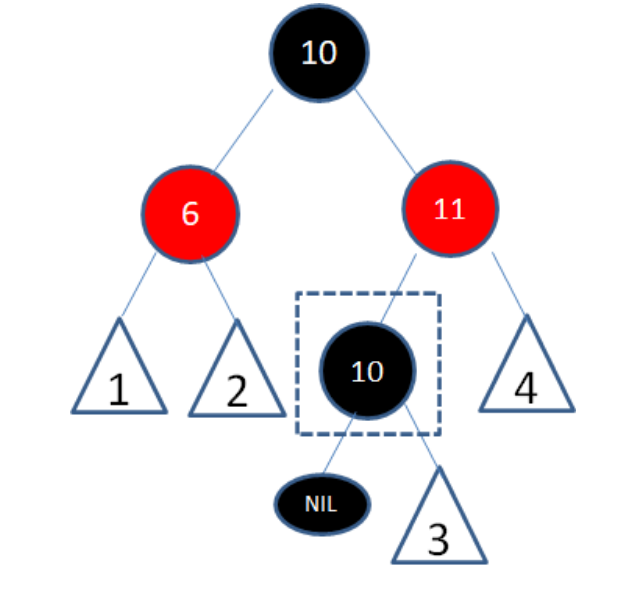
此时10号节点可以等价考虑为一个只有右子树的节点
考虑删除一个只有右子树节点的情况
自身为红色, 子节点为黑色
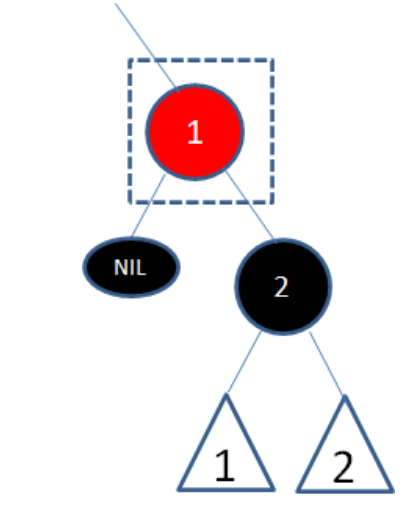
已知删除和插入红色节点都不影响红黑树的性质, 所以直接删除即可
自身为黑色, 子节点为红色
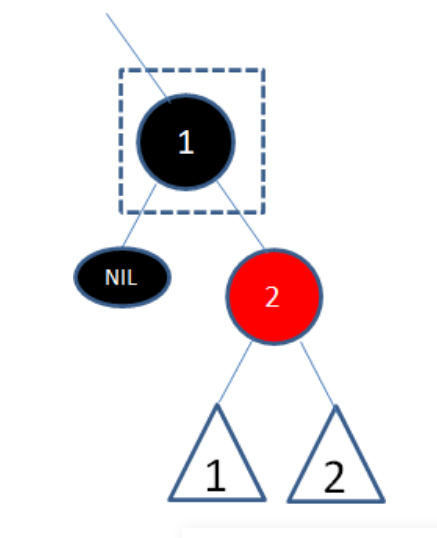
删除自己,然后把儿子涂黑
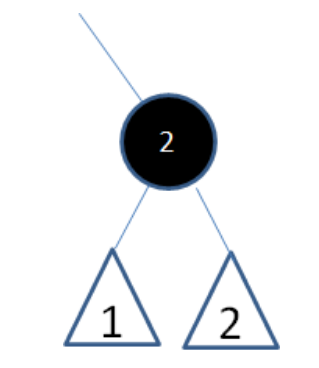
自身为黑色,儿子也为黑色
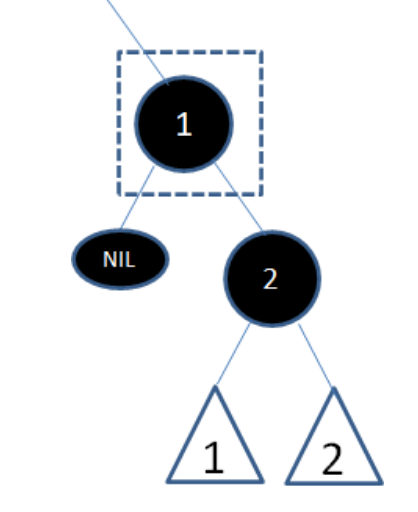
这种情况比较复杂, 因为不能通过向下修改来维护树的平衡
所以要向上递归修改
B树
又叫b-树, 类似于普通的平衡二叉树, 但是允许每个节点有更多的子节点
b树是专门为外部存储器设计的, S