每日一题 week01

报了个 每日一题 希望能坚持下去

day01

统计子矩阵

一眼前缀和+二分

t到怀疑人生

从一开始枚举左上角端点就是个错误

因为当左端点确定后,边界线差不多是这样的

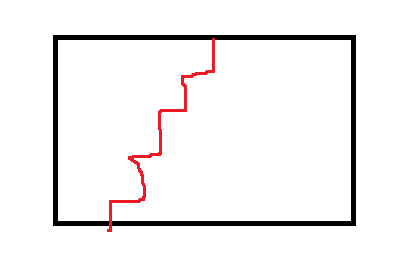
image-20220902001827603

那么这种思路的复杂度就会被卡死在 $n^3logn$ 嘤嘤嘤

题解用了一种很神奇的方法,枚举上边界和下边界,在边界中寻找左右端点

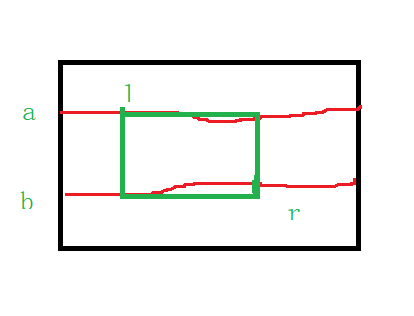
image-20220902002211441

图中(a,l) (b,r)区间内的点即为所求

用双指针就可以把复杂度降到 $n^3$

真神奇

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
/*
    2022/9/1 23:10
    by ergou
*/
#include<bits/stdc++.h>

#define ll long long
#define bug(x) cout<<#x<<"x="<<x<<endl
using namespace std;

const int maxx = 500 + 5;
const int mod = 1e9 + 7;

inline int read() {
    int x = 0, f = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9') {
        if (ch == '-') f = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9') {
        x = x * 10 + ch - 48;
        ch = getchar();
    }
    return x * f;
}

int a[maxx][maxx]={0};
signed main() {
    int n,m,k;

    cin>>n>>m>>k;

    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            cin>>a[i][j];

    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            a[i][j]+=a[i-1][j]+a[i][j-1]-a[i-1][j-1];

    int cnt=0;


    for(int u=1;u<=n;u++)
        for(int d=u;d<=n;d++)
        for(int l=1,r=1;r<=m;r++)
        {
            while(l<=r&&a[d][r]-a[u-1][r]-a[d][l-1]+a[u-1][l-1]>k) l++;
            if(l<=r) cnt+=r-l+1;
        }

    cout<<cnt;
    return 0;
}

题解里有一维优化,大概就是求出每一列前缀和,每次加减都是以 (u,d) 区间内的某一列进行的

想了一下感觉好像不会快很多的样子,而且也不存在空间优化…懒得写了

day02

最多能完成排序的块 II

单调栈

维护每个区间的最大值,如果 x> max ,则x单独成为一个区间

否则需要找到 x 可以插入的区间 (区间合并直到成为第一个区间或者前一个区间的最大值不超过x)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:

    int maxChunksToSorted(vector<int>& arr) {
       stack<int> st;
       for(auto  i:arr)
       {
           if(st.empty()||st.top()<=i)
           st.push(i);
           else
           {
               int m=st.top();
               while(!st.empty()&&st.top()>i) st.pop();
               st.push(m);
           }
           
       }
        return st.size();
    }
};

day03

用户分组

快乐模拟

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    vector<vector<int>> groupThePeople(vector<int>& groupSizes) {
        map<int,vector<int>> mp;
        vector<vector<int>> ans;
        int l=groupSizes.size();
        for(int i=0;i<l;i++)
        {
            if(mp.find(groupSizes[i])==mp.end())
            {
                vector<int> a;
                a.push_back(i);
                mp[groupSizes[i]]=a;
            }
            else mp[groupSizes[i]].push_back(i);

            if( mp[groupSizes[i]].size()==groupSizes[i])
            {
                vector<int> b;
                ans.push_back(mp[groupSizes[i]]);
                mp[groupSizes[i]]=b;
            }
        }

        return ans;
    }
};